|
Найти интервал сходимости ряда и исследовать его сходимость на концах найденного интервала 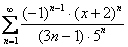
Решение: В общий член степенного ряда входит множитель 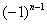 , обеспечивающий знакочередование. Алгоритм решения полностью сохраняется, но при составлении предела , обеспечивающий знакочередование. Алгоритм решения полностью сохраняется, но при составлении предела 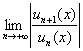 мы игнорируем (не пишем) этот множитель, поскольку модуль уничтожает все «минусы». мы игнорируем (не пишем) этот множитель, поскольку модуль уничтожает все «минусы».
Найдем интервал сходимости данного ряда. Используем признак Даламбера:

Составляем стандартное неравенство:
Ряд сходится при 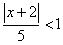
Слева нам нужно оставить только модуль, поэтому умножаем обе части неравенства на 5:
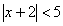
Теперь раскрываем модуль уже знакомым способом:
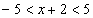
В середине двойного неравенства нужно оставить только «икс», в этих целях из каждой части неравенства вычитаем 2:
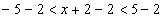
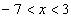 – интервал сходимости исследуемого степенного ряда. – интервал сходимости исследуемого степенного ряда.
Исследуем сходимость ряда на концах найденного интервала:
1) Подставляем значение 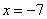 в наш степенной ряд в наш степенной ряд 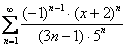 : :

Будьте предельно внимательны, множитель 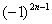 не обеспечивает знакочередование, при любом натуральном «эн» не обеспечивает знакочередование, при любом натуральном «эн» 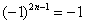 . Полученный минус выносим за пределы ряда и забываем про него, поскольку он (как и любая константа-множитель) никак не влияет на сходимость или расходимость числового ряда. . Полученный минус выносим за пределы ряда и забываем про него, поскольку он (как и любая константа-множитель) никак не влияет на сходимость или расходимость числового ряда.
Итак, требуется исследовать на сходимость числовой ряд 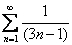 . Здесь проще всего использовать предельный признак сравнения и сравнить данный ряд с расходящимся гармоническим рядом, или . Здесь проще всего использовать предельный признак сравнения и сравнить данный ряд с расходящимся гармоническим рядом, или
Используем интегральный признак.
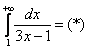
Подынтегральная функция непрерывна на 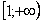 . .
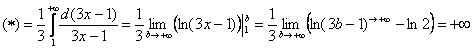
Таким образом, полученный числовой ряд расходится вместе с соответствующим несобственным интегралом.
2) Исследуем второй конец интервала сходимости.
При 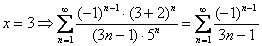
Используем признак Лейбница:
– Ряд является знакочередующимся.
– 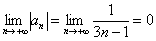 – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий, значит, убывание монотонно. – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий, значит, убывание монотонно.
Вывод: ряд сходится
Рассматриваемый числовой ряд не является абсолютно сходящимся поскольку 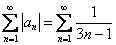 – расходится (по доказанному). – расходится (по доказанному).
Ответ: 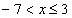 – область сходимости исследуемого степенного ряда, при – область сходимости исследуемого степенного ряда, при 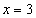 ряд сходится только условно. ряд сходится только условно.
Вы можете заказать решение любых задач по математическому анализу
Примеры на сходимость функциональных рядов
|

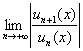 мы игнорируем (не пишем) этот множитель, поскольку модуль уничтожает все «минусы».
мы игнорируем (не пишем) этот множитель, поскольку модуль уничтожает все «минусы».


