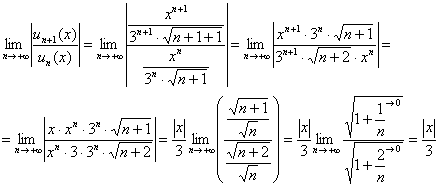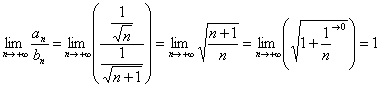Условие и материал
Найти область сходимости степенного ряда 
Решение: Найдем интервал сходимости данного ряда. Используем признак Даламбера:
Составляем стандартное неравенство:
Ряд сходится при 
Слева нам нужно оставить только 
, поэтому умножаем обе части неравенства на 3:
И раскрываем модуль по школьному правилу 
:
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость степенного ряда на концах найденного интервала.
1) При 
Обратите внимание, что при подстановке значения 
в степенной ряд 
у нас сократилась степень 
. Это верный признак того, что мы правильно нашли интервал сходимости ряда.
Исследуем полученный числовой ряд на сходимость.
Используем признак Лейбница.
– Ряд является знакочередующимся.
– 
– члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий, значит, убывание монотонно.
Вывод: Ряд сходится.
Исследуем ряд на абсолютную сходимость:
Сравним данный ряд с расходящимся рядом 
.
Используем предельный признак сравнения:
Получено конечное число, отличное от нуля, значит, ряд 
расходится вместе с рядом 
.
Таким образом, ряд 
сходится только условно.
2) При 
– расходится (по доказанному).
Ответ: Область сходимости исследуемого степенного ряда: 
. При 
ряд сходится только условно.
В рассмотренном примере областью сходимости степенного ряда является полуинтервал, причем во всех точках интервала 
степенной ряд сходится абсолютно , а в точке 
, как выяснилось – сходится только условно.
Вы можете заказать решение любых задач по математическому анализу
Калькулятор сходимости рядов