|
21:34
Найти частные производные
|
|
Калькулятор для нахождения частных производных.
Пример. Найти частные производные функции z = x3-2xy+y2 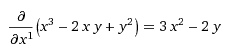
Найдем частную производную по x второго порядка, изменяем порядок 2, получаем ответ:
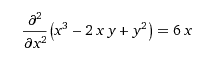
Аналогично находим частную производную первого и второго порядка по y:
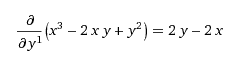
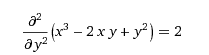
Калькулятор для нахождения смешанных частных производных
Для того чтобы найти смешанную производную по xy, функцию вставляем в калькулятор, указываем переменные x,y ( порядок переменных имеет значение!), получаем:
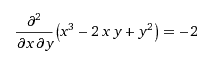
Подведем итог, чем же отличается нахождение частных производных от нахождения «обычных» производных функции одной переменной: 1) Когда мы находим частную производную по x , переменная y считается константой. 2) Когда мы находим частную производную по y, переменная x считается константой. 3) Правила и таблица производных элементарных функций справедливы и применимы для любой переменной , по которой ведется дифференцирование. |
|
|
| Всего комментариев: 1 | |
|
|
|
