Пример. При каких значениях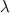 
система 
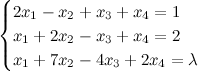будет совместной?
Решение. Ранг
матрицы равен количеству ненулевых строк после приведения этой матрицы к
ступенчатому виду. Поэтому записываем
расширенную матрицу системы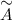
(слева от вертикальной черты находится
матрица системы 
):
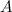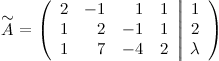
и с помощью элементарных преобразований приводим ее к ступенчатому виду. Для этого вначале от первой строки отнимаем две вторых строки, а от третьей вторую, в результате получаем:
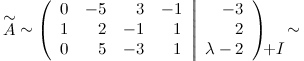
Третью строку складываем с первой:
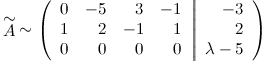
и меняем первую и вторую строки матрицы местами
... Смотреть решение »
