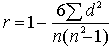Меню сайта
Онлайн калькулятор
| [Дифференциальные уравнение] |
|
Решение дифференциальных уравнений онлайн |
| [Вычислить интеграл] |
|
Решение двойных интегралов онлайн |
| [Исследовать функцию,построить график] |
|
Построить график двух функций онлайн |
| [Решение уравнений] |
|
Решение логарифмических уравнений онлайн |
| [Решение уравнений] |
|
Решение тригонометрических уравнений онлайн |
| [Вычислить интеграл] |
|
Решение определенных интегралов онлайн |
| [Вычислить интеграл] |
|
Найти неопределенный интеграл онлайн |
Наш опрос
Статистика
Поиск
Форма входа
Материалы
| 17.05.2013 [Теоретические моменты] |
|
Центральный момент |
| 10.05.2013 [Теория вероятности] |
|
вероятность безотказной работы |
| 09.05.2013 [Решение контрольных работ] |
|
Решение контрольных работ по физике онлайн |
| 08.05.2013 [Сходимость рядов] |
|
Решение дифференциального уравнения разложить в ря... |
| 08.05.2013 [Сходимость рядов] |
|
Пример решения на сходимость степенного ряда |
| 06.05.2013 [Сходимость рядов] |
|
Найти интервал сходимости степенного ряда |
| 10.04.2013 [решение задач по физике] |
|
Взаимодействие электрических зарядов |
| 08.04.2013 [Решение контрольных работ] |
|
Рещение задач по электричеству |
| 08.04.2013 [решение задач по физике] |
|
определить давление насыщенных паров |
| 08.04.2013 [решение задач по физике] |
|
Определить массу израсходованного газа |
| 08.04.2013 [решение задач по физике] |
|
Дифракционная решетка |
| 08.04.2013 [Решение контрольных работ] |
|
Решение контрольной работы по физике |
| 06.04.2013 [решение задач по физике] |
|
Заряженая частица движется в магнитном поле, сила ... |
Калькулятор
Коэффициент ранговой корреляции Спирмена(по Л.Е.Полякову, 1971)
Коэффициент ранговой корреляции Спирмена - это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.
Практический расчет коэффициента ранговой корреляции Спирмена включает следующие этапы:
1) Сопоставать каждому из признаков их порядковый номер (ранг) по возрастанию (или убыванию).
2) Определить разности рангов каждой пары сопоставляемых значений.
3) Возвести в квадрат каждую разность и суммировать полученные результаты.
4) Вычислить коэффициент корреляции рангов по формуле:.
где ... Смотреть решение »
|
|
Производящая функция Пример 1.Устройство состоит из трёх независимо работающих элементов. Вероятности безотказной работы элементов (за время t) соответственно равны: p1=0,7; р2 = 0,8; р3 = 0,9. Найти вероятности того, что за время t будут работать безотказно: а) все элементы; б) два элемента; в) один элемент; г) ни один из элементов... Смотреть решение » |
|
Как найти уравнение регрессии? Корреляционной зависимостью
|