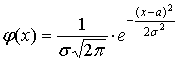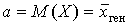Главная » Математическая статистика
Пример 1. Определить доверительный интервал для оценки с надежностью 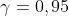 неизвестного математического ожидания  нормально распределенного признака  генеральной совокупности, если известно выборочное среднее 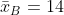 , объем выборки 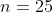 и генеральное среднее квадратическое отклонение 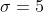
|
Критерии согласия
Для проверки соответствия эмпирического распределения теоретическому (гипотезы) можно наложить на гистограмму теоретическую кривую (рис. 6).
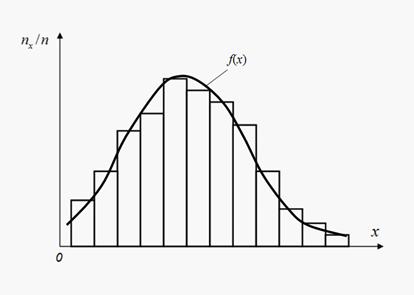
Рис. 6. Гистограмма и теоретическая плотность распределения
При этом неизбежно обнаружатся расхождения, либо случайные, связанные с ограниченным объемом наблюдений, либо свидетельствующие о неправильном подборе выравнивающей функции (гипотезы). Для ответа на этот вопрос используют так называемые «критерии согласия». Для этого вводится случайная величина U, характеризующая расхождение эмпирического и теоретического распределений в предположении истинности теоретического распределения. Мера расхожден... Смотреть решение »
|
Доверительным называется интервал, который с заданной надежностью 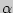 покрывает оцениваемый параметр. покрывает оцениваемый параметр.
Для оценки математического ожидания 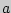 случайной величины случайной величины 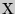 , распределенной по нормальному закону, при известном среднем квадратическом отклонении , распределенной по нормальному закону, при известном среднем квадратическом отклонении 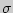 служит доверительный интервал служит доверительный интервал
|
Выборки и доверительные интервалы
Пусть у нас имеется большое количество предметов, с нормальным распределением некоторых характеристик (например, полный склад однотипных овощей, размер и вес которых варьируется). Вы хотите знать средние характеристики всей партии товара, но у Вас нет ни времени, ни желания измерять и взвешивать каждый овощ. Вы понимаете, что в этом нет необходимости. Но сколько штук надо было бы взять на выборочную проверку?
Прежде, чем дать несколько полезных для этой ситуации формул напомним некоторые обозначения.
Во-первых, если бы мы все-таки промерили весь склад овощей (это множество элементов называется генеральной совокупностью... Смотреть решение »
|
Тема "Точечные оценки параметров распределения"
Важной задачей математической статистики является задача оценивания (приближенного определения) по выборочным данным параметров закона распределения признака X генеральной совокупности. Другими словами, необходимо по данным выборочного распределения оценить неизвестные параметры теоретического распределения. Статистические оценки могут быть точечными и интервальными.
Задачу статистического оценивания, а также основные виды статистических оценок, рассмотрим для частного случая: пусть признак X генеральной совокупности распределен нормально, то есть теоретическое распределение имеет вид:
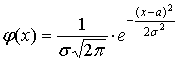
с параметрами: 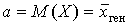 ... Смотреть решение » ... Смотреть решение »
|
|