|
19:20
точечные оценки генеральному среднему и дисперсии
|
||||||||||||
|
Тема "Точечные оценки параметров распределения" Важной задачей математической статистики является задача оценивания (приближенного определения) по выборочным данным параметров закона распределения признака X генеральной совокупности. Другими словами, необходимо по данным выборочного распределения оценить неизвестные параметры теоретического распределения. Статистические оценки могут быть точечными и интервальными. Задачу статистического оценивания, а также основные виды статистических оценок, рассмотрим для частного случая: пусть признак X генеральной совокупности распределен нормально, то есть теоретическое распределение имеет вид:
с параметрами: Точечной оценкой неизвестного параметра называют число (точку на числовой оси), которое приблизительно равно оцениваемому параметру и может заменить его с достаточной степенью точности в статистических расчетах. Точечной оценкой генеральной средней Точечными оценками генеральной дисперсии
Точечными оценками для генерального среднеквадратического отклонения Примеры решения задач Пример 1. Для изучения генеральной совокупности относительно некоторого количественного признака была извлечена выборка:
Найти несмещенные оценки генеральной средней и генеральной дисперсии. Решение. Несмещенной оценкой генеральной средней является выборочная средняя: Ответ: ,
|
||||||||||||
|
|
| Всего комментариев: 0 | |
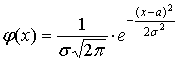
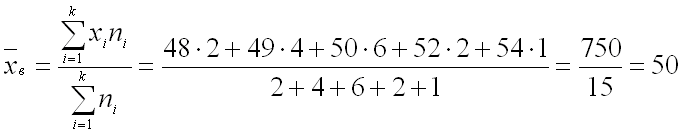 .
.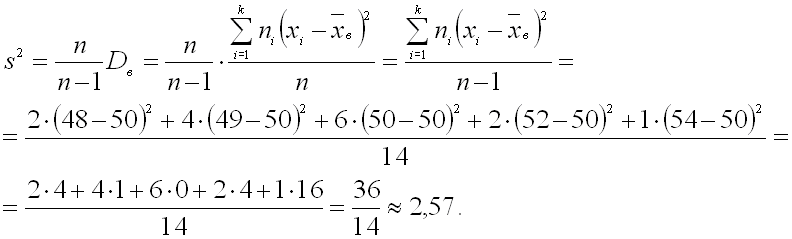
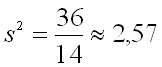 .
.