|
22:08
Нормальный закон распределения
|
Нормальный закон распределенияТеория и примеры решенных задач на нормальный закон распределения Нормальный закон распределения (или распределение Гаусса) задается следующей дифференциальной функцией
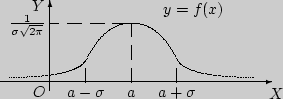
Рис. 56
Пример 1. Показать, что функция Решение. Проверим, что 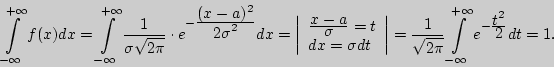 Пример 2. Правило трех сигм. Решение. Найдем вероятность того, что распределенная нормально с.в.
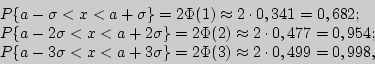 т.е. можно считать практически достоверным, что случайная величина, распределенная по нормальному закону, находится на интервале ] Пример 3. Найти характеристики положения для нормального закона распределения. Решение. 1). 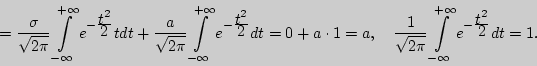 2). 3). Пример 4. Найти характеристики рассеивания для нормального закона распределения. Решение. 1). ![\begin{displaymath} \left\vert {\begin{array}{l} u = t \\ dv = te^{ - {\displ... ...splaystyle t^2\over\displaystyle 2}}dt} } \right] = \sigma ^2. \end{displaymath}](http://cito-web.yspu.org/link1/metod/theory/img910.png) 2). Среднее квадратическое отклонение 3). Найдем асимметрию 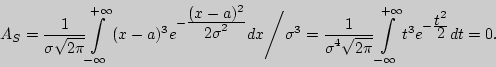 Пример 5. Найти математическое ожидание и дисперсию для показательного двустороннего закона Лапласа. Решение. 1). 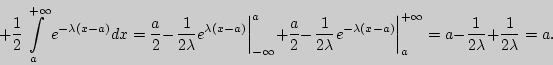 2). Для нахождения дисперсии вычислим M[X ![\begin{displaymath} M[X^2] = \int\limits_{ - \infty }^{ + \infty } {x^2{\display... ...e 2}\int\limits_a^{ + \infty } {x^2e^{ - \lambda (x - a)}dx} = \end{displaymath}](http://cito-web.yspu.org/link1/metod/theory/img917.png) 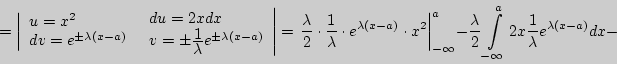 Вопросы для самоконтроля Как задается нормальный закон распределения? Свойства дифференциальной функции распределения нормального закона. Как изменяется кривая нормального распределения при изменении ее параметров? Какие числовые характеристики нормального распределения совпадают? Как можно находить математическое ожидание и среднее квадратичное отклонение по кривой нормального распределения? Каким образом можно получить асимптотическую формулу Лапласа? Правило трех сигм. Задачи I 181. Математическое ожидание нормально распределенной случайной величины 182. Найти плотность вероятности нормально распределенной случайной величины 183. Случайная величина 184. Нормально распределенная случайная величина 185. Случайная величина 186. Случайная величина II 187. Случайная величина 188. Случайная величина III 189. Случайная величина 190. Доказать, что если случайная величина |
|
|
| Всего комментариев: 0 | |
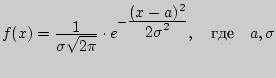 - параметры.
- параметры.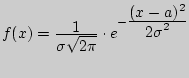 является дифференциальной функцией распределения н.с.в.
является дифференциальной функцией распределения н.с.в.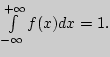
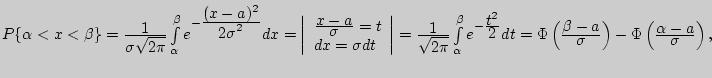 - табличная функция Лапласа .
- табличная функция Лапласа .![$M[X] = {\displaystyle 1\over\displaystyle \sigma \sqrt {2\pi } }\int\limits_{ -... ... + \infty } {e^{ - {\displaystyle t^2\over\displaystyle 2}}(\sigma t + a)dt} = $](http://cito-web.yspu.org/link1/metod/theory/img902.png)
 то
то 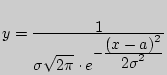 симметричен относительно прямой
симметричен относительно прямой ![$D[X] = {\displaystyle 1\over\displaystyle \sigma \sqrt {2\pi } }\int\limits_{ -... ... \infty }^{ + \infty } {t^2e^{ - {\displaystyle t^2\over\displaystyle 2}}dt} = $](http://cito-web.yspu.org/link1/metod/theory/img909.png)
![$M[X] = \int\limits_{ - \infty }^{ + \infty } {x{\displaystyle \lambda \over\dis... ... \over\displaystyle 2}\int\limits_a^{ + \infty } {xe^{ - \lambda (x - a)}dx} = $](http://cito-web.yspu.org/link1/metod/theory/img914.png)
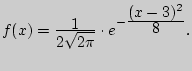 Найти математическое ожидание и дисперсию
Найти математическое ожидание и дисперсию 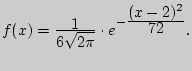 Найти моду и медиану
Найти моду и медиану 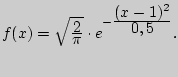 Найти вероятность того, что случайная величина попадет в интервал (0, 2).
Найти вероятность того, что случайная величина попадет в интервал (0, 2).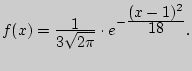 Найти математическое ожидание и дисперсию случайной величины
Найти математическое ожидание и дисперсию случайной величины 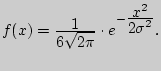 Найти дифференциальную функцию обратной ей величины
Найти дифференциальную функцию обратной ей величины 