Задача. Точка (c,q) наудачу выбирается из квадрата с вершинами (-1,-1), (1,-1), (1,1), (-1,1). Найдите вероятность, что корни уравнения x^2+cx+q=0, будут действительные.
Решение. Условием того, что корни квадратного уравнения x^2+cx+q=0 будут действительные является дискриминант D=c^2-4q≥0.
Изобразим графически
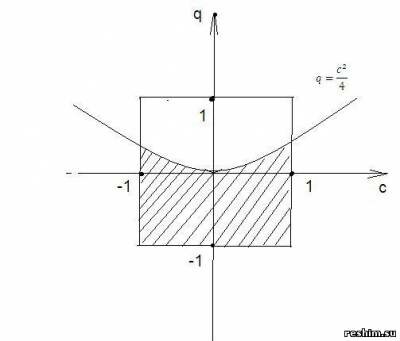
Находим площадь заштрихованной фигуры
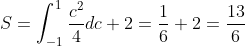
(Вычислить интеграл можно с помощью калькулятора определенных интегралов)
Следовательно, при попадании в заштрихованную область, корни уравнения де ... Смотреть решение »
|
Задача. Функция распределения случайной величины t – времени безотказной работы радиоаппаратуры имеет вид =1-e^{-\frac{t}{3}}) .
Найти:
а) вероятность безотказной работы радиоаппаратуры в течение трех лет;
б) плотность вероятности f (t);
в) математическое ожидание и дисперсию.
Решение.
а) Вероятность события "аппаратура откажет" находим по формуле
События «элемент откажет» и «элемент не откажет»—противоположные, поэтому вероятность того, что элемент не oткaжeт
Вероятность безотказной работы радиоаппаратуры в течение трех лет
=1-F(3)=1-\left&space;(1-e^{-\frac{3}{3}}&space;\right&space;)=e^{-\frac{3}{3}}=1/e)
Заметим также, что
|
Задача 1. В городе имеются 4 оптовые базы. Вероятность того, что требуемого сорта товар отсутствует на этих базах, одинакова и равна 0,3. Составить закон распределения числа баз, на которых искомый товар отсутствует в данный момент.
Решение. 
Задача 2. Вероятность наличия нужной специалисту книги в каждом из 4-ёх магазинов равна 0,1. Составить закон распределения числа магазинов, которые пришлось посетить с целью покупки нужной книги. Найти мат. ожидание, дисперсию этой случайной величины.
Решение.
Последовательно обходим магазины 1 – 2 – 3 – 4.
Вероятность, что в первом же магазине книга будет, равна 0.1. С вероятностью 0.9 идём во второй магазин.
Вероятность, что во втором магазине книга будет, равна 0.1. Абсолютная вероятность этого события равна 0.9*0.1 = 0.09. С вероятностью 0,9 идём в третий магазин. Абсолютная вероятность этого события 0.9*0.9 = 0.81
И так далее. Получим вероятности найти книгу в магазине №:
P(1) = 0.1
P(2) =(1–P(1))*0.1 = 0.9*0.1 = 0.09
P(3) =(1–P(1) –P(2))*0.1 = 0.81*0.1 = 0.081
P(4) =(1–P(1) –P(2) –P(3))*0.1 ... Смотреть решение »
|
« 1 2 ... 12 13 14 15 16 ... 43 44 »
|