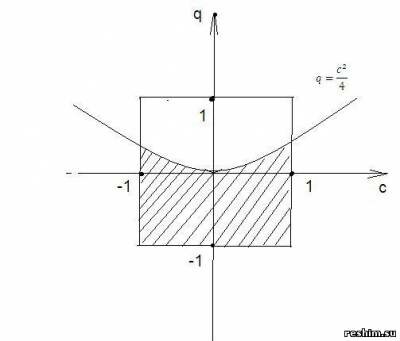
Находим площадь заштрихованной фигуры

(Вычислить интеграл можно с помощью калькулятора определенных интегралов)

1) Если а=0, то уравнение х2+b=0 при b<0 имеет 2 корня, но они - разных знаков, при b=0 имеет 1 корень, при b>0 корней не имеет. Все эти условия нам не подходят. Значит, а отлично от нуля.

2) Далее, если a>0, то ось симметрии параболы у=x2 + ax + b будет находиться слева от оси Оу. Тогда один из возможных корней заведомо будет отрицательным. Нас это не устраивает. Значит, a<0.

3) Если b<0,  то точка пересечения параболы у=x2 + ax + b с осью Оу  будет находиться ниже нуля.Тогда опять один из возможных корней будет отрицательным. А если b=0, то график параболы  у=x2 + ax + b проходит через (0; 0), т.е. корнем будет число 0. Нас и это не устраивает. Поэтому b>0.

3) Т.к. M (a;b) наудачу выбирается из квадрата с вершинами (–1; –1), (1; –1), (1; 1), (–1; 1), то ограничим а и b условиями: -1<a<0 и 0<b<1. 

4) Далее для существования двух корней уравнения  x2 + ax + b = 0 надо проверить, чтобы вершина параболы  у=x2 + ax + b лежала ниже оси Ох.

Последнее неравенство подтверждает то, что  -1<a<0 и 0<b<1. 

Два условия  -1<a<0 и 0<b<1 описыват квадрат, площадь которого равна 1/4 площади квадрата  с вершинами (–1; –1), (1; –1), (1; 1), (–1; 1). Значит, по правилу геометрической вероятности вероятность того, что корни уравнения x2 + ax + b = 0 окажутся действительными и положительными, равна 1/4.