Пример 1. Найти область решений (ОР) и область допустимых решений (ОДР) системы неравенств и определить координаты угловых точек ОДР

                  

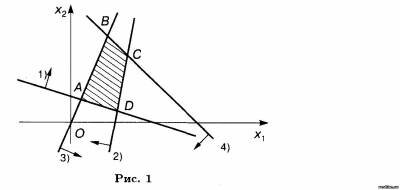
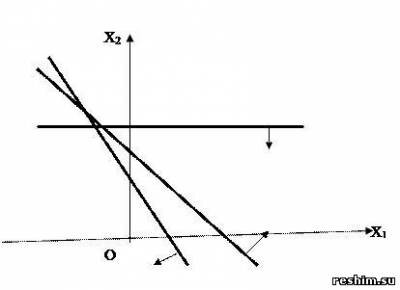
РЕШЕНИЕ. Найдем ОР первого неравенства: X₂ + 3X₂ ≥ 3.

Построим граничную прямую X₁ +3X₂ – 3 = 0 (рис. 1).

Подставим координаты точки (0,0) в неравенство: 1∙0 + 3∙0 > 3; так как координаты точки (0,0) не удовлетворяют ему, то решением неравенства (1) является полуплоскость, не содержащая точку (0,0).

Аналогично найдем решения остальных неравенств системы.

Получим, что ОР и ОДР системы неравенств является выпуклый многогранник ABCD.
 

Найдем угловые точки многогранника. Точку А определим как точку пересечения прямых

Решая систему, получим А(3/7, 6/7). Точку В найдем как точку пересечения прямых

 

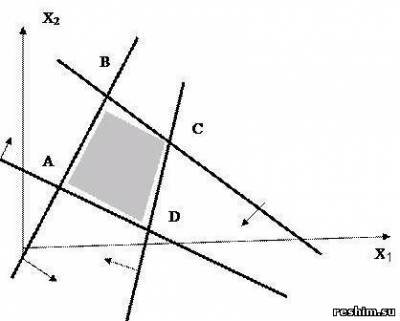
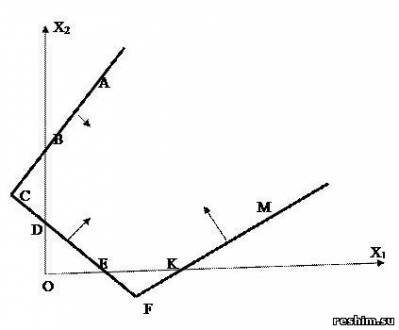
Из системы получим B(5/3, 10/3). Аналогично найдем координаты точек С и D: С(11/4; 9/14), D(3/10; 21/10).

Ответ: ОР и ОДР совпадают, является многоугольник ABCD.

Пример 2 Найти ОР и ОДР системы неравенств и определить координаты угловых точек ОДР.

Решение.

Ответ: А(3/7, 6/7), В(5/3, 10/3), С(11/4, 9/4), D(21/10, 3/10), ОР и ОДР совпадают.

На следующем примере покажем отличие ОР и ОДР

Пример 3. Найти ОР и ОДР системы неравенств

Решение.

Область решения (ОР) системы, удовлетворяющая условиям неотрицательности (xj ≥ 0, j = 1,n), называется областью неотрицательных, или допустимых, решений (ОДР).

Ответ: ACFM – ОР, ABDEKM – ОДР.

Общее решение и область допустимых значений системы неравенств могут иметь одну общую точку, рассмотрим данный случай на следующем примере.

Пример 4.Найти ОР и ОДР системы неравенств

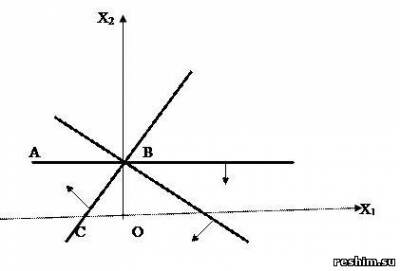
Решение.

Ответ:ABC – ОР, точка B – ОДР.

ОР и ОДР системы несовместные, смотри следующий пример.

Пример 5.Найти ОР и ОДР системы неравенств

Решение.

Ответ: ОР и ОДР несовместны.

Для того, чтобы найти угловые точки: