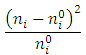Проверка гипотез о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты

Задача. При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты.

РЕШЕНИЕ.

При уровне значимости α=0,05 требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально.

В качестве критерия проверки нулевой гипотезы примем случайную величину («хи квадрат» (критерий согласия Пирсона):

n_i⁰– теоретические частоты;

n_i- эмпирические частоты;

s – число групп (частичных интервалов) выборки.

Выполняем расчетную таблицу, находим χ²_набл:

№	Эмпирические частоты	Теоретические частоты
1	6	4	1
2	12	11	0,09
3	16	15	0,07
4	40	43	0,21
5	13	15	0,27
6	8	6	0,67
7	5	6	0,17
χ2набл			2,47

По таблице критических точек распределения χ²_кр , по заданному уровню значимости α = 0,05  и числу степеней свободы k = s-1-r = s-1-2 = s-3 = 7-3 = 4, где r=2 – число параметров предполагаемого распределения (математическое ожидание и среднее квадратическое отклонение), s=7 – число групп (частичных интервалов) выборки, находим критическую точку χ²_кр(α;k):

χ²_кр(α;k) = χ²_кр(0,05; 4) = 9,49

Если  χ²_набл < χ²_кр  – нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают, считая, что генеральная совокупность не распределена по нормальному закону.