полная производная - 23 Августа 2013 - Примеры решений задач - Решим задачи, контрольные, курсовые...

Главная » 2013 » Август » 23 » полная производная

14:56

полная производная

Как найти полную производную сложной функции?
Производная сложной функции, примеры.

Для того чтобы найти полную производную необходимо уметь находить частные производные.
Для сложной функции двух переменных z=f(x,y), где x=x(u,v), y=y(u,v), частные производные по двум независимым переменным u и v производится по формулам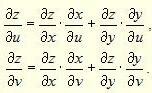

Для сложной функции трех переменных z=f(x,y), где x=x(u,v), y=y(u,v), z=z(u,v), частные производные по двум независимым переменным u и v производится по формулам

Пример 1. Дана сложная функция

$\omega =2^{\frac{xy}{z}},x=\frac{u}{v},y=\sqrt{u},z=v^2+3v$ .

Вычислить производные

$\frac{\partial \omega }{\partial u}, \frac{\partial \omega }{\partial v}$

Решение.

Если задана дифференцируемая по переменным x₁,x₂,...,x_n функция w=f(x₁,x₂,...,x_i,...x_n) и если функции x₁=x₁(t),x₂=x₂(t), ...,x_n=x_n(t) - дифференцируемые функции переменной t , то функция w является сложной дифференцируемой функцией одной переменной t и ее полная производная по независимой переменной t равна:

$\frac{\mathrm{d} \omega }{\mathrm{d} t}=\sum_{i=1}^{n}\frac{\partial \omega }{\partial x_i}\frac{\mathrm{d} x_i}{\mathrm{d} t}$

Иногда функция w явно зависит от t, то есть w=f(t,x₁,x₂,...,x_i,...x_n) в этом случае формула полной производной имеет вид:

$\frac{\mathrm{d} \omega }{\mathrm{d} t}=\frac{\partial \omega }{\partial t}+\sum_{i=1}^{n}\frac{\partial \omega }{\partial x_i}\frac{\mathrm{d} x_i}{\mathrm{d} t}$

Здесь следует различать частную производную $\frac{\partial \omega }{\partial t}$ , которая вычисляется в предположении, что x₁,x₂,...,x_n не зависят от переменной t, и полную производную $\frac{\mathrm{d} \omega }{\mathrm{d} t}$ , которая учитывает зависимость от t функций x₁=x₁(t),x₂=x₂(t), ...,x_n=x_n(t).

Пример 2. Найти полную производную функции:

Всего комментариев: 0