Задача линейной многокритериальной максимизации

   Сформулируем задачу линейной многокритериальной максимизации с двумя переменными и двумя целевыми функциями.

  Пусть на плоскости  задано множество  (Рис. 1) и в каждой точке этого множества определены две непрерывные функции L₁=f₁(x₁, x₂)  и  L₂=f₂(x₁, x₂) . Необходимо найти значения переменных, при которых указанные функции принимают наибольшие значения. Формулировку задачи максимизации с двумя целевыми функциями можно записать более компактно:

f₁(x₁, x₂) → max

... Смотреть решение »

Множество Парето

   Пусть на плоскости (или в пространстве) дано некоторое множество точек M. Точка  называется внутренней точкой множества М, если существует такая окрестность этой точки, которая целиком состоит из точек данного множества.

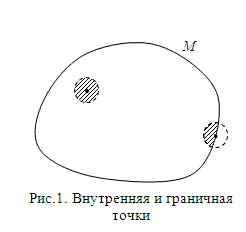
Если же в любой окрестности точки  имеются точки, как принадлежащие, так и не принадлежащие множеству М, то точка  называется граничной точкой множества М.

Совокупность всех граничных точек данного множества М называется его границей.Иллюстрацией служит рис. 1.

  

... Смотреть решение »

Методы решения многокритериальных задач

Метод идеальной точки

Задача линейной многокритериальной максимизации с двумя переменными и двумя целевыми функциями

Пример 1. Найти значения переменных, при которых функции

L₁ = 2x₁ + x₂ + 1 → max

L₂ = x₁ - x₂ + 5 → max

при ограничениях:

x₁ + 2x₂ ≤ 8,

0 ≤ x ≤ 6,

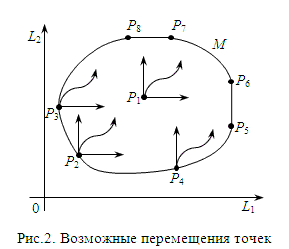
... Смотреть решение »