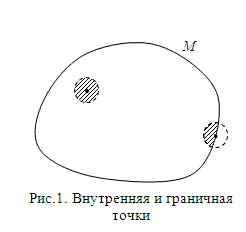
Множество Парето

   Пусть на плоскости (или в пространстве) дано некоторое множество точек M. Точка  называется внутренней точкой множества М, если существует такая окрестность этой точки, которая целиком состоит из точек данного множества.

Если же в любой окрестности точки  имеются точки, как принадлежащие, так и не принадлежащие множеству М, то точка  называется граничной точкой множества М.

Совокупность всех граничных точек данного множества М называется его границей.Иллюстрацией служит рис. 1.

  

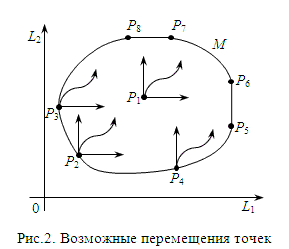
Если множество М не содержит ни одной своей граничной точки, то оно называется открытым (то есть любая точка открытого множества является внутренней).

Если множество М содержит все свои граничные точки, то оно называется замкнутым. В дальнейшем будут рассматриваться только замкнутые множества.

Если множество М не содержит ни одной своей граничной точки, то оно называется открытым (то есть любая точка открытого множества является внутренней).

Если множество М содержит все свои граничные точки, то оно называется замкнутым. В дальнейшем будут рассматриваться только замкнутые множества.

Рассмотрим на плоскости  множество М. Пусть Р — произвольная точка этого множества. Возможно ли во множестве М перемещение точки Р в близкую ей точку так, чтобы при этом увеличились обе ее координаты? Если Р — внутренняя точка, то такое перемещение возможно. Если Р — граничная точка, то такое перемещение не всегда возможно. Иллюстрацией служит рис. 2

Требуемое перемещение точек P₁, P₂ , P₃,P₄ возможно, а ни одна из точек как отрезков  P₅P₆ и P₇P₈, так и дуги  P₆P₇ такому перемещению подвергнута быть не может. Действительно, при перемещении любой точки

• вертикального отрезка  P₅P₆ может увеличиваться лишь координата  L₂ этой точки (координата L₁ при этом останется неизменной);
• горизонтального отрезка P₇P₈  может увеличиваться лишь координата L₁ (координата  L₂ при этом останется неизменной);
• дуги  P₆P₇ увеличение одной координаты влечет уменьшение другой.

Таким образом, каждая точка множества М попадает в один из трех следующих классов.

• Первый класс содержит точки, каждую из которых можно переместить так, чтобы при этом увеличились обе ее координаты, а сама точка осталась во множестве М (в этот класс попадают все внутренние точки множества М и некоторые его граничные точки (например, P₂ )).
• Второй класс содержит точки, каждую из которых можно переместить во множестве М лишь при условии увеличения только одной из ее координат при сохранении значения второй (точки вертикального отрезка  P₅P₆ и точки горизонтального отрезка P₇P₈ ).
• Третий класс содержит точки, каждую из которых можно переместить во множестве М лишь при условии уменьшения хотя бы одной из координат (точки дуги P₆P₇ ).

Множество точек третьего класса называют границей (множеством) Парето данного множества М. Часто говорят, что граница Парето множества М — это множество точек, из которых нельзя переместиться на «север», «восток» или «северо-восток», оставаясь во множестве М.  Считается, что наилучшие решения многокритериальной задачи следует искать именно среди множества Парето. Поэтому построение множества Парето нередко считают первым необходимым шагом в решении любой многокритериальной задачи.