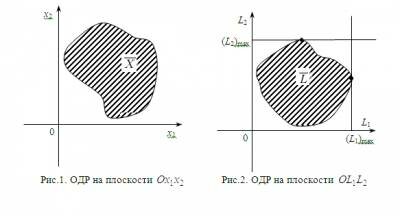
Задача линейной многокритериальной максимизации

   Сформулируем задачу линейной многокритериальной максимизации с двумя переменными и двумя целевыми функциями.

  Пусть на плоскости  задано множество  (Рис. 1) и в каждой точке этого множества определены две непрерывные функции L₁=f₁(x₁, x₂)  и  L₂=f₂(x₁, x₂) . Необходимо найти значения переменных, при которых указанные функции принимают наибольшие значения. Формулировку задачи максимизации с двумя целевыми функциями можно записать более компактно:

f₁(x₁, x₂) → max

f₂(x₁, x₂) → max

при ограничениях:

(x₁, x₂) ϵ

Алгоритм решения многокритериальной задачи:

1) Изобразим на плоскости  все точки, координаты которых удовлетворяют условиям L₁=f₁(x₁, x₂)  и  L₂=f₂(x₁, x₂)  и (x₁, x₂) ϵ . Полученное множество обозначим через  (рис. 2).

    Из рис. 2 видно, что (L₁)_max— наибольшее значение  — L1  и (L₂)_max— наибольшее значение  — L2, достигаются в разных точках. При этом ((L₁)_max,(L₂)_max) .

Это означает, что задача неразрешима — не существует оптимального решения, которое одновременно максимизировало бы обе целевые функции. Поэтому нужно искать Парето-оптимальное решение. Как уже выше отмечалось, наилучшие решения многокритериальной задачи следует искать среди множества Парето. Рассмотрим два метода нахождения недоминируемого решения, связанных с множеством Парето:

1. Метод (последовательных) уступок.
2. Метод идеальной точки (пример).

В рассматриваемом случае множество Парето составлено из допустимых точек задачи, которые не могут быть перемещены в пределах допустимого множества с улучшением сразу по двум критериям: улучшение значения одного критерия влечет ухудшение значения другого.

Метод (последовательных) уступок заключается в том, что лицо принимающее решение (ЛПР) , работая в режиме диалога со специалистом, анализирует точки на границе Парето и выбирает одну из них — компромиссную.

Метод идеальной точки заключается в нахождении на границе Парето точки, ближайшей к точке утопии, задаваемой ЛПР. Как правило, ЛПР формулирует цель в виде определенных показателей, и часто в качестве координат целевой точки выбирается комбинация наилучших значений всех критериев (в данном случае — точка с координатами ((L₁)_max,(L₂)_max). Обычно эта точка не реализуется при заданных ограничениях, поэтому ее и называют точкой утопии.

Замечание. Задачу максимизации можно путем умножения целевой функции на (–1) преобразовать в задачу минимизации, решаемую при тех же самых ограничениях. Это связано с наличием следующего свойства: функция достигает наибольшего значения в тех точках, в которых функция f принимает наименьшее значение, и наоборот. Это означает, что условия [f → min] и [(- f )  → max] равносильны. Следовательно, поменяв знак целевой функции на противоположный, любую двухкритериальную задачу можно свести к задаче максимизации с двумя целевыми функциями.