Задача. Точка (c,q) наудачу выбирается из квадрата с вершинами (-1,-1), (1,-1), (1,1), (-1,1). Найдите вероятность, что корни уравнения x^2+cx+q=0, будут действительные.
Решение. Условием того, что корни квадратного уравнения x^2+cx+q=0 будут действительные является дискриминант D=c^2-4q≥0.
Изобразим графически
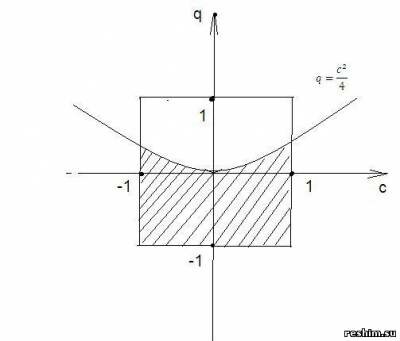
Находим площадь заштрихованной фигуры
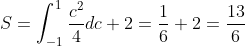
(Вычислить интеграл можно с помощью калькулятора определенных интегралов)
Следовательно, при попадании в заштрихованную область, корни уравнения де ... Смотреть решение »
|
|