|
23:38
закон больших чисел Бернулли
|
|
Получим в качестве следствия из ЗБЧ Чебышёва закон больших чисел Т е о р е м а (ЗБЧ Бернулли). Пусть νn —число успехов в n испытаниях схемы Бернулли с вероятностью успеха p. Тогда
или в эквивалентной форме
См. доказательство. П р и м е р 1. Правильная монета подбрасывается 10000 раз. Оценим См. решение. Пример 2. Оценим вероятность того, что при подбрасывании игральной кости 300 раз относительная частота появления шести очков отклонится от вероятности этого события не более чем на 0,01. Решение. Для оценки события
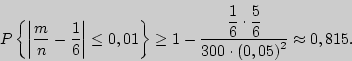 Пример 3. Вероятность того, что изделие является качественным, равна 0,9. Сколько следует проверить изделий, чтобы с вероятностью не меньшей 0,95 можно было утверждать, что абсолютная величина отклонения доли качественных изделий от 0,9 не превысит 0,01? Решение. Воспользуемся неравенством
По условию
Ответ: Пример 4. При контрольной проверке изготавливаемых приборов было установлено, что в среднем 15 шт. из 100 оказывается с теми или иными дефектами. Оценить вероятность того, что доля приборов с дефектами среди 400 изготовленных будет по абсолютной величине отличаться от математического ожидания этой доли не более чем на 0,05. Решение. Воспользуемся неравенством
По условию Итак, Ответ: |
|
|
| Всего комментариев: 0 | |
 При этом для любого ε > 0
При этом для любого ε > 0



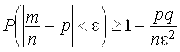 .
.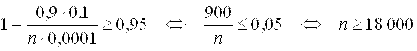 .
.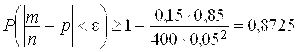 .
.