Операции над множествами

Пример1. Найдем пересечение множеств А = {а, b, с, d, е} и  В  =  {b, d, e, g, к}.

Решение :  Обоим множествам принадлежат элементы b, d, e.
Поэтому А ∩ В = {b, d, e}.

Пояснение. Пересечением множеств A и B называется множество A ∩ B, которое состоит из тех и только тех элементов, которые принадлежат как множеству A, так и множеству B.

Пример 2. Найдем объединение и разность множеств А и В, если
А =  { х| -2/5 ≤ x ≤ 7/3},  В =  { х| -1/4 ≤ x ≤ 3}.

Решение. Если изобразить данные множества на числовой прямой, то
объединение А ∪ В есть часть оси, где имеется хотя бы одна штриховка, т.е.
отрезок [-2/5; 3]. Иначе говоря, А ∪ В = { х| -2/5 ≤ x ≤ 3}.
Разность А\В есть часть отрезка, изображающего множество А,
отмеченная лишь одной штриховкой, т.е. полуинтервал [-2/5; -1/4), точка -1/4
принадлежит В и поэтому не принадлежит А\В.Другими словами,
А\В = { х| -2/5 ≤ x < -1/4}.

Пояснение. Объединением двух множеств A и B называется множество A 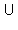 B, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств A или B.

Разностью множеств A и B называется множество A \ B, которое состоит из тех и только тех элементов, которые принадлежат множеству A, но не принадлежат множеству B.

Разность между основным множеством E и множеством A называется дополнением множества A в E и обозначается A'

Пример 3. Известно, что А – множество учащихся, увлекающихся историей, В –
множество учащихся, интересующихся биологией. Сформулируйте условия,
при которых: а) А ∪ В= В; б) А ∩ В = Ø.

Решение: а) выясним, в каком отношении находятся множества А и В.
Известно, что А ∪ В= В, в том случае, когда А ⊂ В, т.е. все элементы
множества А являются также и элементами множества В. Таким образом,
А ∪ В= В, если все учащиеся, увлекающиеся историей, увлекаются и
биологией;
б) Исходя из равенства А ∩ В = Ø множества А и В не пересекаются,
т.е. они не имеют общих элементов. Поэтому А ∩ В =Ø, если все учащиеся,
увлекающиеся историей, не интересуются биологией.