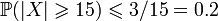Вероятностные неравенства

Т е о р е м а  (неравенство Маркова). Для любого x > 0

См. доказательство.

Грубая оценка случайной величины

Нера́венство Ма́ркова в теории вероятностей даёт оценку вероятности, что случайная величина превзойдёт по модулю фиксированную положительную константу, в терминах её математического ожидания. Получаемая оценка обычно груба. Однако, она позволяет получить определённое представление о распределении, когда последнее не известно явным образом.

Пример 1. В среднем ученики опаздывают на 3 минуты. Какова вероятность того, что ученик опоздает на 15 и более минут? Дайте грубую оценку сверху.

Решение.