Как найти число перестановок с повторениями
Число перестановок c повторениями обозначают
$P( k_1,k_2,...,k_m )$
Сколько же их? Если бы все элементы были различны, то число перестановок равнялось бы $n$. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. В первой группе элементы (первого типа) можно переставлять друг с другом $k_1!$ способами. Но так как все эти элементы одинаковы, то перестановки ничего не меняют. Точно также ничего не меняют $k_2!$ перестановок элементов во второй группе и т. д. Перестановки элементов в разных группах можно делать независимо друг от друга. Поэтому (из принципы умножения) элементы можно переставлять друг с другом $ k_1!*k_2!*...*k_m! $ способами так, что она остаётся неизменной.
Число различных перестановок с повторениями, которые можно составить из данных элементов, равно
$$P(k_1,k_2,...,k_m)=\frac{n!}{k_1!*k_2!*...k_m!}$$
$$n=k_1+k_2+...+k_m $$
Пример 1. Сколькими способами можно нанизать на нить 4 зеленых, 5 синих и 6 красных бус?
... Смотреть решение »
|
Пусть имеется три элемента (n = 3): a, b и c. Тогда из этих трёх элементов можно составить девять размещений с повторениями по два элемента (k = 2): ab, ac, ba, bc, ca, cb, aa, bb, cc (порядок важен!)
Общее число размещениями с повторениями определяется формулой:
или
=m^{k}&space;} "{\color{Blue} {A}_{n}^{k}(k_1,k_2,...k_m)=m^{k} }")
... Смотреть решение »
|
Вычисление сочетаний с повторениями онлайн
Пусть имеется три элемента (n = 3): a, b и c. Тогда из этих трёх элементов можно составить шесть сочетаний с повторениями по два элемента (k = 2): ab, ac, bc, aa, bb, cc (порядок неважен!)
Общее число сочетаний с повторениями определяется по формуле
!}{k!(n-1)!}} "{\color{Blue} \bar{C}_{n}^{k}=C_{n+k-1}^{k}=\frac{(n+k-1)!}{k!(n-1)!}}")
... Смотреть решение »
|
Пример 1. Сколько различных звукосочетаний можно взять на десяти выбранных клавишах рояля, если каждое звукосочетание может содержать от трех до десяти звуков?
Решение. Для звукосочетания клавиши нажимаются одновременно, поэтому для k звуков имеем 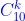 звукосочетаний. Таким образом, искомое количество есть
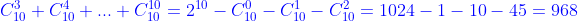
При вычислении было применено третье ... Смотреть решение »
|
Свойства сочетаний
|
|
