|
18:12
Задача на классическую вероятность
|
|
Задача. Какова вероятность того, что среди вынутых наудачу 4 карт из полной колоды 52 карт ровно две окажутся принадлежащими пиковой масти?
РЕШЕНИЕ
1) Для вычисления вероятности появления данного события воспользуемся классическим определением вероятности события, согласно которому вероятность определяется по формуле: 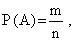 где m – число исходов, при которых появляется событие А, n – общее число элементарных несовместных равновозможных исходов. 2) Определим n. Для этого воспользуемся формулой сочетания по 4 из 52(так как нас не интересует порядок вытянутых карт): 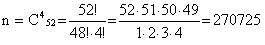 3) Обозначим событие А = «Из 4 вынутых карт 2 принадлежат пиковой масти». Найдем вероятность вытягивания 2 пиковых карт по формуле сочетания по 2 из 13 (так как всего карт пиковой масти 13): 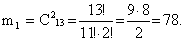 4) Найдем вероятность вытягивания оставшихся двух карт не пиковой масти по формуле сочетания по 2 из 39 (52-13). 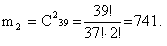 5) Полученные значения мы перемножаем: m = m1 и m2
m = 78 * 741 = 57798
6) Найдем вероятность того, что среди вынутых наудачу 4 карт из полной колоды 52 карт ровно две окажутся принадлежащими пиковой масти: 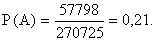 ОТВЕТ: Вероятность того, что среди вынутых наудачу 4 карт из полной колоды 52 карт ровно две окажутся принадлежащими пиковой масти, равна 0,21. Онлайн сервис: решение задач по теории вероятности |
|
|
| Всего комментариев: 0 | |
