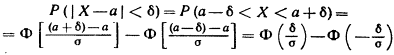2.2. Вычисление вероятности заданного отклонения

Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной вели­чины Х по абсолютной величине меньше заданного положительного числа d, т. е. требуется найти вероятность осуществления неравенства  |x —а|<d.

Заменим это неравенство равносильным ему двойным неравенством

Тогда получим:

Приняв во внимание равенство:

(функция Лапласа—нечетная), окончательно имеем

Вероятность заданного отклонения равна

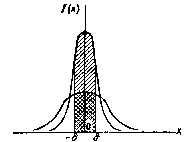
На рисунке наглядно показано, что если две случайные величины нормально распределены и а = 0, то вероятность принять значение, принадлежащее интервалу (-d,d),больше у той величины, которая имеет меньшее значение d. Этот факт полностью соответствует вероятностному смыслу параметра s .

Пример. Случайная величина Х распределена нормально. Математическое ожидание и среднее квадратическое отклонение Х соответственно равны 20 и 10. Найти вероятность того, что отклонение по абсолютной величине будет меньше трех.

Решение: Воспользуемся формулой

 По условию ,

тогда

Онлайн сервис:  решение задач по теории вероятности