|
22:46
Составить закон распределения, Найти математическое ожидание и дисперсию
|
||||||||||||||||
|
Задача. Игральная кость брошена два раза. Составить закон распределения случайной величины Х – числа появления двойки. Найти математическое ожидание и дисперсию случайной величины.
РЕШЕНИЕ
1) Составим закон распределения случайной величины Х:
2) Найдем вероятность события А = «При бросании кости выпала двойка». Для вычисления вероятности появления данного события воспользуемся классическим определением вероятности события, согласно которому вероятность определяется по формуле: 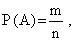 где m – число исходов, при которых появляется событие А, n – общее число элементарных несовместных равновозможных исходов.  В нашем случае m = 1, а n = 6 (так как на кости шесть граней с числами). Тогда   3) Для определения вероятностей того, что двойка выпадет 0, 1 или 2 раза воспользуемся формулой Бернулли:  4) Найдем вероятность того, что двойка на игральной кости не выпадет ни разу (Х=0).  5) Найдем вероятность того, что двойка на игральной кости выпадет один раз (Х=1).  6) Найдем вероятность того, что двойка на игральной кости выпадет два раза (Х=2).  7) Заполним теперь таблицу, выражающую закон распределения случайной величины Х:
8) Определим математическое ожидание данной случайной величины Х (математическое ожидание характеризует среднее значение случайной величины при большом числе испытаний): 
М(Х) = 0 * 0,694 + 1 * 0,278 + 2 * 0,028 = 0,334.
9) Определим дисперсию для данной случайной величины по формуле (дисперсия характеризует средний квадрат отклонения случайной величины от среднего):     10) Определим среднеквадратическое отклонение, которое характеризует среднее отклонение случайной величины от среднего, по формуле:   ОТВЕТ: Математическое ожидание случайной величины равно М(Х) = 0,334. Дисперсия случайной величины равна Д(Х) = 0,278. Онлайн сервис: решение задач по теории вероятности |
||||||||||||||||
|
|
| Всего комментариев: 0 | |
