|
15:17
динамика вращательного движения
|
Задача 1Однородный диск радиусом R = 0,2 м и массой m = 5 кг вращается вокруг оси, проходящей через его центр перпендикулярно к его плоскости. Зависимость угловой скорости ϖ вращения диска от времени t дается уравнением ϖ = A + Bt, где В=8 рад/с2 . Найти касательную силу, приложенную к ободу диска. Трением пренебречь.Решение.  Задача 2
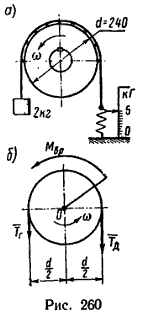
Для определения мощности электродвигателя через его шкив перекинута тормозная лента (рис. 260, а). Один конец ленты удерживается динамометром, а к другому концу прикреплена двухкилограммовая гиря. После запуска двигателя при установившейся угловой скорости n=1850 об/мин динамометр показывает усилие 49 Н. Определить мощность двигателя. Решение задачи1. Рассмотрим, какие силы действуют на шкив при установившемся равномерном вращении. Шкив приводится во вращательное движение вращающим моментом Mвр, создаваемым двигателем. Кроме того, на шкив действуют сила натяжения правой ветви ленты, создаваемая динамометром (Tд=49 Н), и сила Tг натяжения левой ветви ленты, создаваемая двухкилограммовой гирей (Tг=2*9,81=19,6 Н) (рис. 260, б).
2. Определим вращающий момент двигателя. Так как шкив вращается равномерно, то алгебраическая сумма моментов всех сил относительно оси вращения шкива равна нулю: 3. Переведя угловую скорость n=1850 об/мин в рад/сек: Таким образом, мощность двигателя составляет 685 вт. Задача 3 |
|
|
| Всего комментариев: 0 | |