Меню сайта
Наш опрос
Обмен ссылками
Статистика
Поиск
Форма входа
Материалы
| 06.02.2013 [Математическая статистика] |
|
уравнение регрессии |
| 06.02.2013 [Математическая статистика] |
|
выборочный коэффициент корреляции |
| 05.02.2013 [Исследовать функцию,построить график] |
|
Построить график двух функций онлайн |
| 05.02.2013 [Вычислить интеграл] |
|
Решение двойных интегралов онлайн |
| 04.02.2013 [Решение уравнений] |
|
Решение логарифмических уравнений онлайн |
| 04.02.2013 [Вычислить интеграл] |
|
Найти неопределенный интеграл онлайн |
| 04.02.2013 [Вычислить интеграл] |
|
Решение определенных интегралов онлайн |
| 04.02.2013 [Решение уравнений] |
|
Решение тригонометрических уравнений онлайн |
| 04.02.2013 [Дифференциальные уравнение] |
|
Решение дифференциальных уравнений онлайн |
| 02.02.2013 [решение задач по физике] |
|
эффект Комптона |
Калькулятор
Главная » Мат анализ » Пределы » Задача 2.
Задание. Найти предел функции
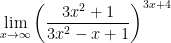
Решение.
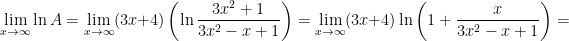
Используем, что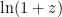 при
при 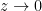 . Здесь
. Здесь
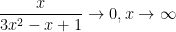
так как старшая степень числителя (1) меньше степени знаменателя (2). Поэтому
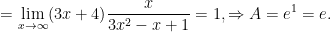
Способ 2.
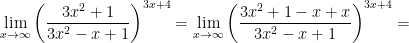
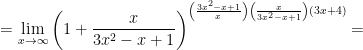
Используем второй замечательный предел 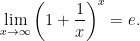
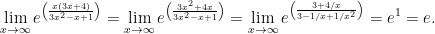
Задание. Найти предел функции
Решение.
Способ 1. Преобразуем выражение к экспоненте в сложной степени и вычислим предел, к которому стремится показатель степени.
Рассмотрим
Используем, что
так как старшая степень числителя (1) меньше степени знаменателя (2). Поэтому
Способ 2.

