Меню сайта
Наш опрос
Обмен ссылками
Статистика
Форма входа
Материалы
| 06.02.2013 [Математическая статистика] |
|
уравнение регрессии |
| 06.02.2013 [Математическая статистика] |
|
выборочный коэффициент корреляции |
| 05.02.2013 [Исследовать функцию,построить график] |
|
Построить график двух функций онлайн |
| 05.02.2013 [Вычислить интеграл] |
|
Решение двойных интегралов онлайн |
| 04.02.2013 [Решение уравнений] |
|
Решение логарифмических уравнений онлайн |
| 04.02.2013 [Вычислить интеграл] |
|
Найти неопределенный интеграл онлайн |
| 04.02.2013 [Вычислить интеграл] |
|
Решение определенных интегралов онлайн |
| 04.02.2013 [Решение уравнений] |
|
Решение тригонометрических уравнений онлайн |
| 04.02.2013 [Дифференциальные уравнение] |
|
Решение дифференциальных уравнений онлайн |
| 02.02.2013 [решение задач по физике] |
|
эффект Комптона |
Калькулятор
Главная » Мат анализ » Пределы » Задача 1.
Задача. Найти предел последовательности![\dpi{100} \lim_{n \to \infty }(\sqrt[3]{n^{6}-6n^{4}+1}-n^{2})](http://latex.codecogs.com/gif.latex?%5Cdpi%7B100%7D%20%5Clim_%7Bn%20%5Cto%20%5Cinfty%20%7D%28%5Csqrt[3]%7Bn%5E%7B6%7D-6n%5E%7B4%7D+1%7D-n%5E%7B2%7D%29)
Решение.
![\dpi{100} \lim_{n \to \infty }(\sqrt[3]{n^{6}-6n^{4}+1}-n^{2})=](http://latex.codecogs.com/gif.latex?%5Cdpi%7B100%7D%20%5Clim_%7Bn%20%5Cto%20%5Cinfty%20%7D%28%5Csqrt[3]%7Bn%5E%7B6%7D-6n%5E%7B4%7D+1%7D-n%5E%7B2%7D%29=)
![\dpi{100} =\lim_{n \to \infty }\frac{(\sqrt[3]{n^{6}-6n^{4}+1}-n^{2})((n^{6}-6n^{4}+1)^{2/3}+n^{4}+n^{2}\sqrt[3]{n^{6}-6n^{4}+1})}{(n^{6}-6n^{4}+1)^{2/3}+n^{4}+n^{2}\sqrt[3]{n^{6}-6n^{4}+1}}=](http://latex.codecogs.com/gif.latex?%5Cdpi%7B100%7D%20=%5Clim_%7Bn%20%5Cto%20%5Cinfty%20%7D%5Cfrac%7B%28%5Csqrt[3]%7Bn%5E%7B6%7D-6n%5E%7B4%7D+1%7D-n%5E%7B2%7D%29%28%28n%5E%7B6%7D-6n%5E%7B4%7D+1%29%5E%7B2/3%7D+n%5E%7B4%7D+n%5E%7B2%7D%5Csqrt[3]%7Bn%5E%7B6%7D-6n%5E%7B4%7D+1%7D%29%7D%7B%28n%5E%7B6%7D-6n%5E%7B4%7D+1%29%5E%7B2/3%7D+n%5E%7B4%7D+n%5E%7B2%7D%5Csqrt[3]%7Bn%5E%7B6%7D-6n%5E%7B4%7D+1%7D%7D=)
Упрощаем по формуле разности кубов:
![\dpi{100} =\lim_{n \to \infty }\frac{-6n^{4}+1}{(n^{6}-6n^{4}+1)^{2/3}+n^{4}+n^{2}\sqrt[3]{n^{6}-6n^{4}+1}}=](http://latex.codecogs.com/gif.latex?%5Cdpi%7B100%7D%20=%5Clim_%7Bn%20%5Cto%20%5Cinfty%20%7D%5Cfrac%7B-6n%5E%7B4%7D+1%7D%7B%28n%5E%7B6%7D-6n%5E%7B4%7D+1%29%5E%7B2/3%7D+n%5E%7B4%7D+n%5E%7B2%7D%5Csqrt[3]%7Bn%5E%7B6%7D-6n%5E%7B4%7D+1%7D%7D=)
![\dpi{100} =\lim_{n \to \infty }\frac{-6+\frac{1}{n^{4}}}{(1-\frac{6}{n^{2}}+\frac{1}{n^{6}})^{2/3}+1+\sqrt[3]{1-\frac{6}{n^{2}}+\frac{1}{n^{6}}}}=\frac{-6}{1+1+1}=-2](http://latex.codecogs.com/gif.latex?%5Cdpi%7B100%7D%20=%5Clim_%7Bn%20%5Cto%20%5Cinfty%20%7D%5Cfrac%7B-6+%5Cfrac%7B1%7D%7Bn%5E%7B4%7D%7D%7D%7B%281-%5Cfrac%7B6%7D%7Bn%5E%7B2%7D%7D+%5Cfrac%7B1%7D%7Bn%5E%7B6%7D%7D%29%5E%7B2/3%7D+1+%5Csqrt[3]%7B1-%5Cfrac%7B6%7D%7Bn%5E%7B2%7D%7D+%5Cfrac%7B1%7D%7Bn%5E%7B6%7D%7D%7D%7D=%5Cfrac%7B-6%7D%7B1+1+1%7D=-2)
Мы учитываем, что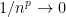 при
при 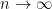 (
( 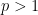 — число, степень).
— число, степень).
Задача. Найти предел последовательности
Решение.
Получаем неопределенность вида 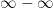 . Поэтому умножаем и делим, на выражение, дополняющее до полного куба (чтобы избавится от кубического корня):
. Поэтому умножаем и делим, на выражение, дополняющее до полного куба (чтобы избавится от кубического корня):
Упрощаем по формуле разности кубов:
Получаем неопределенность вида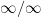 . Делим числитель и знаменатель на старшую степень
. Делим числитель и знаменатель на старшую степень 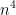 :
:
Мы учитываем, что

