|
10:41
Решение задачи по теории вероятностей
|
|
Условие задачи. Игральная кость брошена дважды. 1. Описать пространство элементарных событий Ω. 2. Описать пространство элементарных событий, если его элементами служат суммы выпавших очков. 3. Назвать элементы Ω, составляющие события: ● A — сумма очков равна 7; ● B — хотя бы на одной кости выпала 1; ● C — сумма очков делится на 3. 4. Описать словами события: ● D = {(11),(12),(21)}; ● E = {(46), (55), (64)}. 5. Изобразить события A, B, C, D, E на диаграмме Эйлера-Венна. Решение задачи. 1. Ω = {11,12,13,14,15,16, 21, 22,..., 66}, 2. Ω = {2,3,4,5,6, 7,8,9,10,11,12}
3. ● A = {16,61,34, 43, 25, 52};
● B = {11,12, 21,13,31,14, 41,15, 51,16, 61} ● C = {12, 21,36,63,45, 54,33,15, 51, 24,42,66}. ● D = {СУММА ОЧКОВ РАВНА 2 ИЛИ 3 }; ● E = {СУММА ОЧКОВ РАВНА 10}. 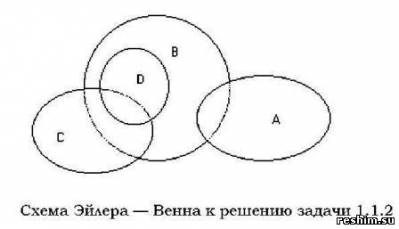 |
|
|
| Всего комментариев: 0 | |
