|
23:13
Решение задачи линейнрго программирования графическим методом
|
Задача. Фирма выпускает 2 вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются два исходных продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы даны в табл. 20.1.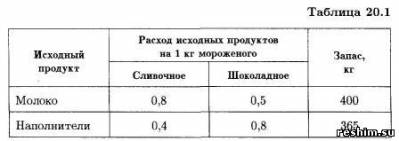 Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более чем на 100 кг. Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Розничная цена 1 кг сливочного мороженого 16 р., шоколадного — 14 р. Какое количество мороженого каждого вида должна производить фирма, чтобы доход от реализации продукции был максимальным?
РЕШЕНИЕ. Обозначим: x1 — суточный объем выпуска сливочного мороженого, кг; x2 — суточный объем выпуска шоколадного мороженого, кг. Составим математическую модель задачи. Целевая функция будет иметь вид При ограничениях:
OABDEF — область допустимых решений (рис. 20.1). Находим вектор с:
Строим вектор с(16, 14). Линия уровня L0 задается уравнением
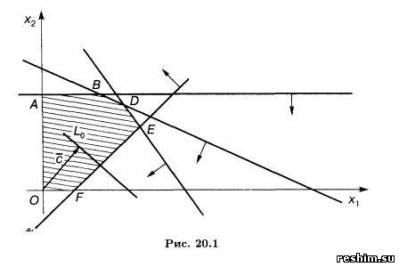 Перемещаем линию уровня по направлению вектора с. Точкой выхода L0 из области допустимых решений является точка D, ее координаты определяются как пересечение прямых, заданных уравнениями: Решая систему, получим координаты точки D (312,5; 300), в которой и будет оптимальное решение, т.е.
при этом Таким образом, фирма должна выпускать в сутки 312,5 кг сливочного мороженого и 300 кг шоколадного мороженого, при этом доход от реализации составит 9 200 р. |
|
|
| Всего комментариев: 0 | |
