Интегрирование заменой
Во многих случаях удается введением новой переменной t вместо переменной интегрирования x свести данный интеграл к новому интегралу, который или содержится в таблице основных интегралов, или легко вычисляется другим способом. Такой метод называется методом замены переменной или методом подстановки.
Формула интегрирования заменой переменной:
dx=\int&space;f\left&space;\left&space;[&space;\varphi&space;\left&space;(&space;t&space;\right&space;)&space;\right&space;]\varphi&space;'\left&space;(&space;t&space;\right&space;)dt "\int f(x)dx=\int f\left \left [ \varphi \left ( t \right ) \right ]\varphi '\left ( t \right )dt")
На примерах рассмотрим:
Алгоритм интегрирования заменой переменной
Пример 1. Найти интеграл
^{10}dx "\int \left ( 3x+2 \right )^{10}dx")
Решение.
1) Замена: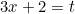 
... Смотреть решение »