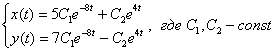Линейные однородные системы дифференциальных уравнений

Простейшая однородная система дифференциальных уравнений имеет следующий вид:

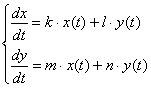
Пример 1

Решить задачу Коши для системы дифференциальных уравнений 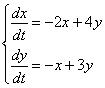 с начальными условиями , .

Решение:

Решим систему методом исключения. Напоминаю, что суть метода – свести систему к одному дифференциальному уравнению.

Алгоритм решения стандартен:

1) Берем второе уравнение системы  и выражаем из него :
   

2) Дифференцируем по  обе части полученного уравнения :

Со «штрихами» процесс выглядит так:

Важно, чтобы этот простой момент был понятен, далее я не буду на нём останавливаться.

3) Подставим  и  в первое уравнение системы :

И проведём максимальные упрощения:

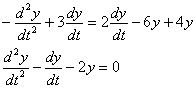
Получено самое что ни на есть обычное однородное уравнение второго порядка с постоянными коэффициентами. Со «штрихами» оно записывается так: .

Составим и решим характеристическое уравнение:

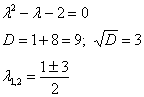
 – получены различные действительные корни, поэтому:
.

4) Идём за функцией . Для этого берём уже найденную функцию  и находим её производную. Дифференцируем по :

Подставим  и  в уравнение (*):

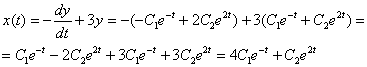
Или короче:

5) Обе функции найдены, запишем общее решение системы:

6) Найдем частное решение, соответствующее начальным условиям  , :

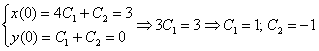
Здесь из первого уравнения я почленно вычел второе уравнение,

Ответ: частное решение: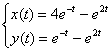

Полученный ответ достаточно легко проверить, проверку осуществим в три шага:

1) Проверяем, действительно ли выполняются начальные условия  , :

Оба начальных условия выполняются.

2) Проверим, удовлетворяет ли найденный ответ первому уравнению системы .

Берём из ответа функцию  и находим её производную:

Подставим ,   и  в первое уравнение системы:

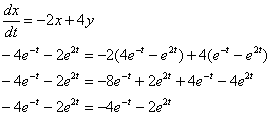
Получено верное равенство, значит, найденный ответ удовлетворяет первому уравнению системы.

3) Проверим, удовлетворяет ли ответ второму уравнению системы

Берём из ответа функцию  и находим её производную:

Подставим ,   и  во второе уравнение системы:

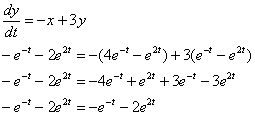
Получено верное равенство, значит, найденный ответ удовлетворяет второму уравнению системы.

Линейные неоднородные системы дифференциальных уравнений

Практически то же самое, только решение будет несколько длиннее.

Неоднородная система дифференциальных уравнений, которая в большинстве случаев может встретиться вам в задачах, имеет следующий вид:

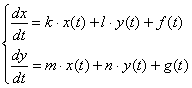
По сравнению с однородной системой в каждом уравнении дополнительно добавляется некоторая функция, зависящая от «тэ». Функции  могут быть константами (причем, по крайне мере одна из них не равна нулю), экспонентами, синусами, косинусами и т.д.

Пример 3

Найти частное решение системы линейных ДУ, соответствующее заданным начальным условиям

Решение: Дана линейная неоднородная система дифференциальных уравнений, в качестве «добавок»  выступают константы. Используем метод исключения, при этом сам алгоритм решения полностью сохраняется. Для разнообразия я начну как раз с первого уравнения.

1) Из первого уравнения системы выражаем:
  

2) Дифференцируем по  обе части:

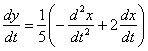
Константа (тройка) исчезла, ввиду того, что производная константы равна нулю.

3) Подставим  и 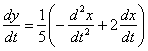 во второе уравнение системы :

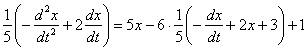
Сразу после подстановки целесообразно избавиться от дробей, для этого каждую часть уравнения умножаем на 5:

Теперь проводим упрощения:

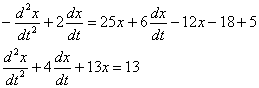
В результате получено линейное неоднородное уравнение второго порядка с постоянными коэффициентами. Вот, по сути, и всё отличие от решения однородной системы уравнений, разобранного в предыдущем параграфе.

Примечание: Тем не менее, в неоднородной системе иногда может получиться и однородное уравнение.

Найдем общее решение соответствующего однородного уравнения:

Составим и решим характеристическое уравнение:

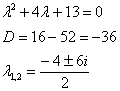
 – получены сопряженные комплексные корни, поэтому:
.

Частное решение неоднородного уравнения ищем в виде .
Найдем первую и вторую производную:

Подставим  в левую часть неоднородного уравнения:

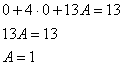
Таким образом:

Следует отметить, что частное решение  легко подбирается устно, и вполне допустимо вместо длинных выкладок написать: «Очевидно, что частное решение неоднородного уравнения: ».

В результате:

4) Ищем функцию . Сначала находим производную от уже найденной функции :

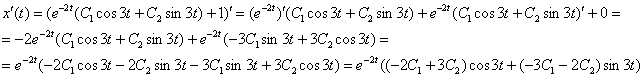
Подставим  
и  в уравнение (*):

5) Общее решение системы:

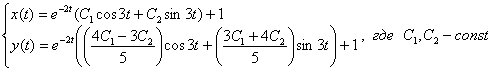
6) Найдем частное решение, соответствующее начальным условиям :

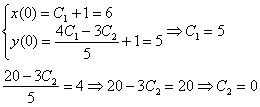
Окончательно, частное решение:

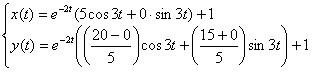
Ответ: частное решение: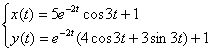

Метод характеристического уравнения (метод Эйлера)

Пример 5

Дана линейная однородная система дифференциальных уравнений

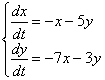
Найти общее решение системы уравнений с помощью характеристического уравнения

Решение: Смотрим на систему уравнений и составляем определитель второго порядка:

По какому принципу составлен определитель, думаю, всем видно.

Составим характеристическое уравнение, для этого из каждого числа, которое располагается на главной диагонали, вычитаем некоторый параметр :

На чистовике, естественно, сразу следует записать характеристическое уравнение, я объясняю подробно, по шагам, чтобы было понятно, что откуда взялось.

Раскрываем определитель:

И находим корни квадратного уравнения:

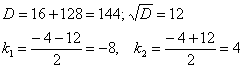
Если характеристическое уравнение имеет два различных действительных корня, то общее решение системы дифференциальных уравнений имеет вид:

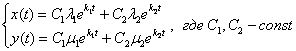
Коэффициенты в показателях экспонент  нам уже известны, осталось найти коэффициенты

1) Рассмотрим корень  и подставим его в характеристическое уравнение:

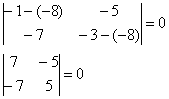
(эти два определителя на чистовике тоже можно не записывать, а сразу устно составить нижеприведенную систему)

Из чисел  определителя составим систему двух линейных уравнений с двумя неизвестными:

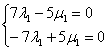
Из обоих уравнений следует одно и то же равенство:

Теперь нужно подобрать наименьшее значение , такое, чтобы значение  было целым. Очевидно, что следует задать . А если , то

2) Всё аналогично. Рассмотрим корень  и устно подставим его в характеристическое уравнение:

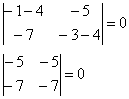
Из чисел  определителя составим систему:

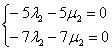
Из обоих уравнений следует равенство:

Подбираем наименьшее значение , таким образом, чтобы значение  было целым. Очевидно, что .

Все четыре коэффициента  найдены, осталось их подставить в общую формулу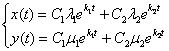

Ответ: общее решение: