|
19:14
Перестановки по кругу на плоскости и в пространстве
|
|
Задача. Семь девушек водят хоровод. Сколькими различны ми способами они могут встать в круг? Решение. Если бы они стояли на месте, то получилось бы Pn=P7=7! = 5040 перестановок. Но так как танцующие кружатся, то их положение относительно окружающих предметов не существенно, а важно лишь взаимное расположение. Поэтому перестановки, переходящие друг в друга при кружении танцовщиц надо считать одинаковыми. Но из каждой перестановки можно получить еще шесть новых путем вращения. Значит, число 5040 надо разделить на 7. Мы получаем 5040:7=720 различных перестановок девушек в хороводе. Вообще, если рассматривать перестановки n предметов, расположенных не в ряд, а по кругу, и считать одинаковыми расположения, переходящие друг в друга при вращении, то число различных перестановок равно (n-1)!. А теперь сосчитаем, сколько ожерелий можно составить из 7 различных бусин? По аналогии с только что решенной задачей можно подумать, что число различимых ожерелий равно 720. Но ожерелье можно не только повернуть по кругу, но и перевернуть (см.рис.). 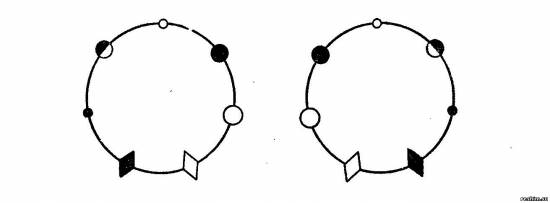 Поэтому ответом на эту задачу является 720 : 2=360. |
|
|
| Всего комментариев: 1 | |
|
|
|
