|
20:22
Интегрирование рациональных функций
|
|
Интегрирование элементарных дробей. Каждая рациональная функция на каждом промежутке, принадлежащем ее области определения, представима в виде суммы многочлена и элементарных рациональных дробей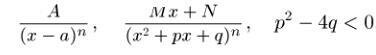 Поэтому интегрирование рациональных функций сводится к разложению рациональной функции на элементарные дроби и к интегрированию элементарных дробей и многочленов. Интегрирование элементарных дробей производится следующим образом: Из формул 1)-4) следует, что интеграл от элементарной дроби выражается через рациональные функции, логарифмы и арктангенсы. Поэтому неопределенный интеграл от любой рациональной функции на всяком промежутке, принадлежащем ее области определения, является элементарной функцией, представимой в виде алгебраической суммы композиций рациональных функций, логарифмов и арктангенсов. Пример 1. Найти интеграл рациональной функции Решение.  Пример 2. Найти интеграл рациональной функции Решение.  Пример 3. Найти интеграл Решение.  Пример 4. Найти интеграл Решение.  Пример 5. Найти интеграл Решение.  Заключение. Вся сложность интегрирования рациональных функций заключается в разложении функции на элементарные дроби. Для проведения данной математической операции предлагаем калькулятор. |
|
|
| Всего комментариев: 0 | |

