|
10:31
Комбинаторика. Теория множеств
|
|
Условие задачи. По каналу связи последовательно передано три знака. Описать пространство элементарных событий и события:
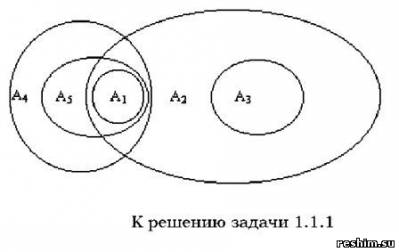
1. принят только первый знак; 2. принят, по крайней мере, один знак; 3. приняты два и только два знака; 4. принято меньше двух знаков; 5. принят один знак Решение задачи. Используем цифры 0, 1 для обозначения событий: 0 - знак искажен, 1 - знак принят. Тогда пространство элементарных событий запишется в виде • Ω={000, 100,010,001, 110, 101,011, 111} и имеет размерность восемь. • Событие A1 - принят только первый знак: A1 = {100}; • Событие A2 - принят по крайней мере один знак: • A2 = {100 + 010 + 001 + 110 + 101 + 011 + 111} = Ω\{000}; • Событие A3 - приняты два и только два знака: A3 = {110 + 011 + 101}; • Событие A4 - принято меньше двух знаков: A4 = {000 + 100 + 010 + 001}; • Событие A5 — принят один знак: A5 = {100 + 010 + 001}. Из полученных результатов следует, что 1. события A1 и A3 - несовместные 2. события A4, A3 - несовместные 3. события A3, A5 - несовместные 4. A5 влечет A4 (A5 ⊂ A4) 5. события A1 и A2 - совместны, 6. A2 и A3, A1 и A4, A1 и A5, A2 и A4 — совместные; 7. A3 ⊂ A2 ; A1 ⊂ A5 ⊂ A4 A1 = A5 + A2.
Изобразим эти события на схеме Эйлера-Венна.(1.5)
 |
|
|
| Всего комментариев: 0 | |
